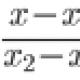Закон накопления погрешностей. Накопление погрешности

при численном решении алгебраических уравнений - суммарное влияние округлений, сделанных на отдельных шагах вычислительного процесса, на точность полученного решения линейной алгебраич. системы. Наиболее распространенным способом априорной оценки суммарного влияния ошибок округления в численных методах линейной алгебры является схема т. н. обратного анализа. В применении к решению системы линейных алгебраич. уравнений схема обратного анализа заключается в следующем. Вычисленное прямым методом Мрешение хуи не удовлетворяет (1), но может быть представлено как точное решение возмущенной системы Качество прямого метода оценивается по наилучшей априорной оценке, к-рую можно дать для норм матрицы и вектора. Такие "наилучшие"и наз. соответственно матрицей и вектором эквивалентного возмущения для метода М. Если оценки для и имеются, то теоретически ошибка приближенного решения может быть оценена неравенством Здесь - число обусловленности матрицы А, а матричная норма в (3) предполагается подчиненной векторной норме В действительности оценка для редко бывает известна, и основной смысл (2) состоит в возможности сравнения качества различных методов. Ниже приводится вид нек-рых типичных оценок для матрицы Для методов с ортогональными преобразованиями и арифметики с плавающей запятой (в системе (1) Аи bсчитаются действительными) В этой оценке - относительная точность арифметич. операций в ЭВМ,- евклидова матричная норма, f(n) - функция вида, где п- порядок системы. Точные значения константы Си показателя kопределяются такими деталями вычислительного процесса, как способ округления, использование операции накопления скалярных произведений и т. д. Наиболее часто k=1 или 3/2. В случае методов типа Гаусса в правую часть оценки (4) входит еще множитель, отражающий возможность роста элементов матрицы Ана промежуточных шагах метода по сравнению с первоначальным уровнем (такой рост отсутствует в ортогональных методах). Чтобы уменьшить значение, применяют различные способы выбора ведущего элемента, препятствующие возрастанию элементов матрицы. Для квадратного корня метода, к-рый применяется обычно в случае положительно определенной матрицы А, получена наиболее сильная оценка Существуют прямые методы (Жордана, окаймления, сопряженных градиентов), для к-рых непосредственное применение схемы обратного анализа не приводит к эффективным оценкам. В этих случаях при исследовании Н. п. применяются и иные соображения (см. - ). Лит.: Givens W., "TJ. S. Atomic Energy Commiss. Repts. Ser. OR NL", 1954, № 1574; Wilkinson J. H., Rounding errors in algebraic processes, L., 1963; Уилкинсон Д ж.
Для устойчивых методов характерен рост погрешности как Оценка погрешности таких методов обычно производится следующим образом. Строится уравнение относительно возмущения, вносимого или округлением, или погрешностями метода и затем исследуется решение этого уравнения (см. , ). В более сложных случаях применяется метод эквивалентных возмущений (см. , ), развитый в отношении задачи исследования накопления вычислительной погрешности при решении дифференциальных уравнений (см. , , ). Вычисления по нек-рой расчетной схеме с округлениями рассматриваются как вычисления без округлений, но для уравнения с возмущенными коэффициентами. Сравнивая решение исходного сеточного уравнения с решением уравнения с возмущенными коэффициентами получают оценку погрешности. Уделяется существенное внимание выбору метода по возможности с меньшими значениями qи A(h). При фиксированном методе решения задачи расчетные формулы обычно удается преобразовать к виду, где (см. , ). Это особенно существенно в случае обыкновенных дифференциальных уравнений, где число шагов в отдельных случаях оказывается очень большим. Величина (h)может сильно расти с ростом промежутка интегрирования. Поэтому стараются применять методы по возможности с меньшим значением A(h). В случае задачи Коши ошибка округления на каждом конкретном шаге по отношению к последующим шагам может рассматриваться как ошибка в начальном условии. Поэтому нижняя грань (h)зависит от характеристики расхождения близких решений дифференциального уравнения, определяемого уравнением в вариациях. В случае численного решения обыкновенного дифференциального уравнения уравнение в вариациях имеет вид и потому при решении задачи на отрезке (х 0 , X)нельзя рассчитывать на константу A(h)в мажорантной оценке вычислительной погрешности существенно лучшую, чем Поэтому при решении этой задачи наиболее употребительны однощаговые методы типа Рунге - Кутта или методы типа Адамса (см. , ), где Н. п. в основном определяется решением уравнения в вариациях. Для ряда методов главный член погрешности метода накапливается по подобному закону, в то время как вычислительная погрешность накапливается существенно быстрее (см. ). Область практич. применимости таких методов оказывается существенно уже. Накопление вычислительной погрешности существенно зависит от метода, применяемого для решения сеточной задачи. Напр., при решении сеточных краевых задач, соответствующих обыкновенным дифференциальным уравнениям, методами стрельбы и прогонки Н. п. имеет характер A(h)h-q, где qодно и то же. Значения A(h)у этих методов могут отличаться настолько, что в определенной ситуации один из методов становится неприменимым. При решении методом пристрелки сеточной краевой задачи для уравнения Лапласа Н. п. имеет характер с 1/h, с>1, а в случае метода прогонки Ah-q. При вероятностном подходе к исследованию Н. п. в одних случаях априорно предполагают какой-то закон распределения погрешности (см. ), в других случаях вводят меру на пространстве рассматриваемых задач и, исходя из этой меры, получают закон распределения погрешностей округления (см. , ). При умеренной точности решения задачи мажорантные и вероятностные подходы к оценке накопления вычислительной погрешности обычно дают качественно одинаковые результаты: или в обоих случаях Н. п. происходит в допустимых пределах, или в обоих случаях Н. п. превосходит такие пределы. Лит.: Воеводин В. В., Вычислительные основы линейной алгебры, М., 1977; Шура-Бура М. Р., "Прикл. матем. и механ.", 1952, т. 16, № 5, с. 575-88; Бахвалов Н. С, Численные методы, 2 изд., М., 1975; Уилкинсон Дж. X., Алгебраическая проблема собственных значений, пер. с англ., М.. 1970; Бахвалов Н. С, в кн.: Вычислительные методы и программирование, в. 1, М., 1962, с, 69-79; Годунов С. К., Рябенький В. С, Разностные схемы, 2 изд., М., 1977; Бахвалов Н. С, "Докл. АН СССР", 1955, т. 104, № 5, с. 683-86; его же, "Ж. вычислит, матем. и матем. физики", 1964; т. 4, № 3, с. 399- 404; Лапшин Е. А., там же, 1971, т. 11, № 6, с.1425-36. Н. С. Бахвалов.

Смотреть значение Накопление Погрешности в других словарях

Накопление — накопления, ср. (книжн.). 1. только ед. Действие по глаг. накопить-накоплять и накопиться-накопляться. воды. Первоначальное накопление капитала (исходный пункт создания........
Толковый словарь Ушакова

Накопление Ср. — 1. Процесс действия по знач. глаг.: накопить, накопиться. 2. Состояние по знач. глаг.: накопить, накопиться. 3. То, что накоплено.
Толковый словарь Ефремовой

Накопление — -я; ср.
1. к Накопи́ть - накопи́ться. Н. богатств. Н. знаний. Источники накопления.
2. только мн.: накопле́ния. То, что накоплено; сбережения. Увеличить размеры накоплений........
Толковый словарь Кузнецова

Накопление — - 1. увеличение личных капиталов, запасов, имущества; 2.
доля национального
дохода, используемая на пополнение производственных и непроизводственных фондов в........
Экономический словарь

Накопление - Accumulation — Ситуация, при которой происходит
рост торговых позиций, созданных ранее. Обычно это происходит за
счет добавления вновь открываемых позиций к уже существующим.........
Экономический словарь

Накопление Валовое — приобретение товаров, произведенных в отчетном
периоде, но не потребленное.
Показатель
счета
Операции с капиталом системы национальных счетов включает........
Экономический словарь

Накопление Дивиденда — В страховании жизни: способ урегулирования, содержащийся в условиях полиса по страхованию жизни, предоставляющий возможность оставить на депозитном счете страховой........
Экономический словарь

Накопление Инвестором Менее 5% Акций Компании, Являющейся Целью Перекупки — Как только приобретается 5% акций,
покупатель должен представить информацию в Комиссию по ценным
бумагам и
биржам, на соответствующую биржу и в компанию,........
Экономический словарь

Накопление Основного Капитала Валовое — вложение средств в основной капитал основные(фонды) для создания нового дохода в будущем.
Экономический словарь

Накопление Основного Капитала, Валовое — - вложение средств в
основной
капитал (
основные фонды) для создания нового
дохода в будущем. В.н.о.к. состоит из следующих элементов: а)
приобретение........
Экономический словарь

Накопление Страховое — ENDOWMENT INSURANCEФорма страхования жизни, сочетающая
СТРАХОВАНИЕ и обязательное
накопление. Отличается от обычного страхования жизни тем, что по истечении определенного........
Экономический словарь

Накопление, Аккумулирование — Финансирование корпораций: прибыль, которая не выплачивается в качестве дивидендов, а добавляется к основному капиталу компании. См. также accumulated profits tax. Инвестиции:........
Экономический словарь

Привлечение, Накопление, Образование Капитала; Прирост Основного Капитала — Создание или расширение путем накопления сбережений капитала или средств производства (producers goods) - зданий, оборудования, механизмов - необходимых для производства ряда........
Экономический словарь

Накопление — - превращение части прибыли в капитал, увеличение запасов материалов, имущества, денежных средств, наращивание капитала, основных средств государством, предприятиями,........
Юридический словарь

Накопление — использование части дохода для расширения производства иувеличения на этой основе выпуска продукции и услуг. Размеры накопления итемпы его роста зависят от объема........

Первоначальное Накопление Капитала — процесс превращения основной массымелких товаропроизводителей (главным образом крестьян) в наемных рабочихпутем отделения их от средств производства и превращения........
Большой энциклопедический словарь

Погрешности Измерений — (ошибки измерений) - отклонения результатовизмерений от истинных значений измеряемой величины. Систематическиепогрешности измерений обусловлены главным образом........
Большой энциклопедический словарь

Погрешности Средств Измерений — отклонения метрологических свойств илипараметров средств измерений от номинальных, влияющие на погрешностирезультатов измерений (создающие т. н. инструментальные ошибки измерений).
Большой энциклопедический словарь

Первоначальное Накопление — - процесс превращения основной массы мелких товаропроизводителей, в основном крестьян, в наемных рабочих. Создание предпринимателями накоплений для последующей организации........
Исторический словарь

Первоначальное Накопление — накопление капитала, предшествующее капиталистич. способу производства, делающее этот способ производства исторически возможным и составляющее его отправной, исходный........
Советская историческая энциклопедия

Валовое Накопление Основного Капитала — вложение резидентными единицами средств в объекты основного капитала для создания нового дохода в будущем путем использования их в производстве. Валовое накопление основного капитала........
Социологический словарь

Измерение Ориентированное На Индикатор Погрешности — - англ. measurement, indicator error,-oriented; нем. Fehlermessung. По В. Торгерсону - измерение, направленное на выявление в реакции опрашиваемых информации об индикаторах или раздражителях,........
Социологический словарь

Капитала Накопление — - англ. capital accumulation; нем. Akkumulation. Превращение прибавочной стоимости в капитал, происходящее в процессе расширенного воспроизводства.
Социологический словарь

Капитала Накопление Первоначальное — - англ. capital accumulation, primitive; нем. Akkumulation, urprungliche. Предшествующий капиталист, способу производства процесс отделения непосредственных производителей (гл. обр. крестьян)........
Социологический словарь

Капитальное Накопление — (capital accumulation) - см Накопление капитала.
Социологический словарь

Накопление (или Расширенное Воспроизводство) Капитала — (accumulation (or expanded or extended reproduction) of capital) (марксизм) - процесс, в ходе которого капитализм развивается посредством найма рабочей силы для производства прибавочной........
Социологический словарь

Первоначальное Накопление — (primitive accumulation) (Марксизм) - исторический процесс, посредством которого был накоплен капитал прежде, чем появился капитализм. В "Das Kapital" Маркс задается вопросом,........
Социологический словарь

Временное Накопление Отходов На Пром-площадке — - хранение отходов на территории предприятия в специально обустроенных для этих целей местах до момента их использования в последующем технологическом цикле или отправки........
Экологический словарь

НАКОПЛЕНИЕ — НАКОПЛЕНИЕ, -я, ср. 1. см. копить, -ся. 2. мн. Накопленная сумма, количество чего-н. Большие накопления. || прил. накопительный, -ая, -ое (спец.). Накопительная ведомость.
Толковый словарь Ожегова

БИОЛОГИЧЕСКОЕ НАКОПЛЕНИЕ — БИОЛОГИЧЕСКОЕ НАКОПЛЕНИЕ концентрирование (накопление) ряда химических веществ (пестицидов, тяжелых металлов, радионуклидов и др.) в трофических........
Экологический словарь

Аналитическая химия

УДК 543.08+543.422.7

ПРОГНОЗИРОВАНИЕ ПОГРЕШНОСТЕЙ ФОТОМЕТРИИ С ИСПОЛЬЗОВАНИЕМ ЗАКОНА НАКОПЛЕНИЯ ОШИБОК И МЕТОДА МОНТЕ-КАРЛО

В.И. Голованов, ЕМ Данилина

В вычислительном эксперименте, при сочетании закона распространения ошибок и метода Монте-Карло, исследовано влияние погрешностей приготовления растворов, погрешностей холостого опыта и погрешностей измерения пропускания на метрологические характеристики фотометрического анализа. Найдено, что результаты прогнозирования погрешностей аналитическим и статистическим методами взаимосогласованы. Показано, что особенностью метода Монте-Карло является возможность прогнозирования закона распределения погрешностей в фотометрии. На примере сценария рутинного анализа рассмотрено влияние гетероскедастичности разброса вдоль градуировочного графика на качество анализа.

Ключевые слова: фотометрический анализ, закон накопления ошибок, градуировочный график, метрологические характеристики, метод Монте-Карло, стохастическое моделирование.

Введение

Прогнозирование погрешностей фотометрического анализа в основном строят на использовании закона накопления ошибок (ЗНО) . Для случая линейной формы закона светопогло-щения: - 1§Т = А = в1с, ЗНО обычно записывают уравнением:

8А _ 8С _ 0,434-10^

А ‘8Т-

При этом стандартное отклонение измерения степени пропускания предполагается постоянным во всем динамическом интервале фотометра. Вместе с тем, как отмечают в , кроме аппаратурных погрешностей на точность анализа влияют погрешность холостого опыта, погрешность настройки пределов шкалы прибора, кюветная погрешность, химические факторы, погрешность установки аналитической длины волны. Эти факторы считают основными источниками погрешности результата анализа. Вкладами в накопленную погрешность точности приготовления градуировочных растворов обычно пренебрегают.

Отсюда видим, что уравнение (1) не имеет существенной прогностической силы, поскольку учитывает влияние только одного фактора. Кроме того, уравнение (1) является следствием приближенного разложения закона светопоглощения в ряд Тейлора. Отсюда возникает вопрос о его точности, обусловленной пренебрежением членами разложения выше первого порядка. Математический анализ остатков разложения сопряжен с вычислительными трудностями и в практике химического анализа не применяется.

Целью данной работы является изучение возможности применения метода Монте-Карло (метода статистических испытаний) в качестве независимого метода для изучения и прогнозирования накопления погрешностей фотометрического анализа, дополняющего и углубляющего возможности ЗНО.

Теоретическая часть

В этой работе будем полагать, что итоговая случайная погрешность градуировочной функции обусловлена не только инструментальными погрешностями измерения оптической плотности, но и погрешностями настройки шкалы прибора на 0 и 100 % пропускания (погрешность хо-

лостого опыта), а также погрешностями приготовления градуировочных растворов. Другими, названными выше, источниками погрешностей пренебрегаем. Тогда перепишем уравнение закона Бугера-Ламберта-Бэра в удобной для дальнейшего построения форме:

Аы = кс" + А

В этом уравнении с51 - концентрации головного стандартного раствора окрашенного вещества, аликвоты (Уа) которого разбавляют в колбах с номинальным объёмом Уд для получения градуировочной серии растворов, Аы - оптическая плотность раствора холостого опыта. Поскольку при фотометрировании оптическую плотность испытуемых растворов измеряют относительно холостого раствора, т. е. Аы принимают за условный нуль, то Аы = 0. (Заметим, что измеренное при этом значение оптической плотности можно называть условной экстинкцией.) В уравнении (2) безразмерная величина с" имеет смысл концентрации рабочего раствора, выраженной в единицах концентрации головного стандарта. Коэффициент к назовем экстинкцией стандарта, поскольку А§1 = е1с81 при с" = 1.

Применим к выражению (2) оператор закона накопления случайных ошибок, полагая Уа, Уд и Аы случайными величинами. Получаем:

Еще одной независимой случайной величиной, влияющей на разброс значений А, является степень пропускания, поскольку

А = -1§Т, (4)

поэтому к дисперсиям в левой части уравнения (3) добавляем еще одно слагаемое:

52а=(0,434-10а)Ч+8Іьі +

В этой окончательной записи закона накопления ошибок постоянны абсолютные стандартные отклонения Т, Аы и Уд, а для Уа постоянна относительная стандартная погрешность.

При построении стохастической модели градуировочной функции на основе метода Монте-Карло считаем, что возможные значения х* случайных величин Т, Аы Уа и Уд, распределены по нормальному закону. Согласно принципу Монте-Карло, возможные значения будем разыгрывать по методу обратной функции :

X; =М(х1) + р-1(г])-вХ|, (6)

где М(х) - математическое ожидание (действительное значение) переменной, ¥(г^) - функция Лапласа-Гаусса, ц - возможные значения равномерно распределенной на интервале (0,1) случайной величины Я, т. е. случайные числа, зх - стандартное отклонение соответствующей переменной, \ = 1...т - порядковый номер независимой случайной величины. После подстановки выражения (6) в уравнения (4) и (2) имеем:

А" = -18Хі=-1810-а +Р-1(г])8т,

где А" = "к-+ х2

Вычисления по уравнению (7) возвращают отдельную реализацию градуировочной функции, т.е. зависимость А" от математического ожидания М(с") (номинального значения с"). Поэтому запись (7) является аналитическим выражением случайной функции . Сечения этой функции получают при многократном разыгрывании случайных чисел в каждой точке градуировочной зависимости. Выборочную совокупность реализаций обрабатывают методами математической статистики с целью оценивания генеральных параметров градуировки и проверки гипотез о свойствах генеральной совокупности.

Очевидно, что рассматриваемые нами два подхода к проблеме прогнозирования метрологических характеристик в фотометрии - на основе ЗНО, с одной стороны, и на основе метода Монте-Карло, с другой, должны дополнять друг друга. В частности, из уравнения (5) можно получить результат при гораздо меньшем, по сравнению с (7), объёме вычислений, а также проранжиро-

вать случайные величины по значимости их вкладов в результирующую погрешность. Ранжирование позволяет отказаться от отсеивающего эксперимента при статистических испытаниях и априори исключить из рассмотрения малозначимые переменные. Уравнение (5) несложно проанализировать математически для того, чтобы судить о характере вкладов факторов в общую дисперсию. Частные вклады факторов можно подразделить на независящие от А, либо возрастающие с увеличением оптической плотности. Поэтому sA как функция А должна быть монотонно возрастающей зависимостью, лишенной минимума. При аппроксимации экспериментальных данных уравнением (5) частные вклады одинакового характера будут смешиваться, например, юоветная погрешность может смешиваться с погрешностью холостого опыта. С другой стороны, при статистических испытаниях модели методом Монте-Карло можно выявить такие важные свойства градуировочного графика как закон (законы) распределения погрешностей, а также оценить быстроту сходимости выборочных оценок к генеральным. На основе ЗНО такой анализ невозможен.

Описание вычислительного эксперимента

При построении имитационной модели градуирования полагаем, что градуировочная серия растворов приготовлена в мерных колбах с номинальной вместимостью 50 мл и предельной погрешностью +0,05 мл. В серию колб добавляют от 1 до 17 мл головного стандартного раствора с погрешностью пипетирования > 1 %. Погрешности измерения объёмов оценивали по справочнику . Аликвоты вносят с равномерным шагом 1 мл. Всего в серии 17 растворов, оптическая плотность которых охватывает интервал от 0,1 до 1,7 ед. Тогда в уравнении (2) коэффициент к = 5. Погрешность холостого опыта принимаем на уровне 0,01 ед. оптической плотности. Погрешности измерения степени пропускания, согласно , зависят только от класса прибора и находятся в интервале от 0,1 до 0,5 % Т.

Для большей привязки условий вычислительного эксперимента к лабораторному эксперименту воспользовались данными по воспроизводимости измерений оптических плотностей растворов К2Сг207 в присутствие 0,05 М H2S04 на спектрофотометре СФ-26. Авторы аппроксимируют экспериментальные данные на интервале А = 0,1... 1,5 уравнением параболы:

sBOCn*103 =7,9-3,53A + 10,3A2. (8)

Нам удалось подогнать расчеты по теоретическому уравнению (5) к расчетам по эмпирическому уравнению (8) с использованием оптимизационного метода Ньютона. Нашли, что уравнение (5) удовлетворительно описывает эксперимент при s(T) = 0,12 %, s(Abi) = 0,007 и s r(Va) = 1,1 %.

Приведенные в предыдущем абзаце независимые оценки погрешностей хорошо согласуются с найденными при подгонке. Для вычислений по уравнению (7) создана программа в виде формы листа электронных таблиц MS Excel. Наиболее существенной особенностью нашей Excel-программы является использование выражения НОРМСТОБР(СЛЧИС()) для генерирования нормально распределенных погрешностей, см. уравнение (6). В специальной литературе по статистическим вычислениям в Excel подробно описана утилита «Генерация случайных чисел», которую во многих случаях предпочтительно заменять на функции типа НОРМСТОБР(СЛЧИС()). Такая замена особенно удобна при создании собственных программ для моделирования методом Монте-Карло.

Результаты и их обсуждение

Прежде чем приступать к статистическим испытаниям, оценим вклады слагаемых в левой части уравнения (5) в общую дисперсию оптической плотности. Для этого каждое слагаемое нормируют на общую дисперсию. Расчеты выполнены при s(T) = 0,12%, s(Aw) = 0,007, Sr(Va)=l,l % и s(Vfi) = 0,05. Результаты вычислений показаны на рис. 1. Видим, что вкладами в общую дисперсию погрешностей измерения Vfl можно пренебречь.

Тогда как вклады другой, влияющей на погрешности приготовления растворов, величины Va

доминируют в интервале оптических плотностей 0,8__1,2. Однако этот вывод не имеет общего

характера, поскольку при измерениях на фотометре с s(T) = 0,5 % погрешности градуировки, согласно расчету, определяются главным образом, разбросом Аы и разбросом Т. На рис. 2 сравниваются относительные ошибки измерений оптических плотностей, прогнозируемых на основе ЗНО (сплошная линия) и метода Монте-Карло (значки). При статистических испытаниях кривую

ошибок восстанавливали по 100 реализациям градуировочной зависимости (1700 значениям оптических плотностей). Видим, что оба прогноза взаимно согласованы. Точки равномерно группируются возле теоретической кривой. Однако даже при таком, довольно внушительном, статистическом материале полной сходимости не наблюдается. Во всяком случае, разброс не позволяет выявить приближенный характер ЗНО, см. введение.

0 0.4 0.8 1.2 1.6

Рис. 1. Весовые вклады слагаемых уравнения (5) в дисперсию А: 1 - для Аы; 2 - для Уа; 3 - для Т; 4 - для

Рис. 2. Кривая погрешностей градуировочного графика

Из теории математической статистики известно , что при интервальном оценивании математического ожидания случайной величины надежность оценивания повышается, если известен закон распределения для этой величины. Кроме того, в случае нормального распределения оценка является наиболее эффективной. Поэтому исследование закона распределения погрешностей градуировочного графика является важной задачей. При таком исследовании, прежде всего, проверяют гипотезу нормальности разброса оптических плотностей в отдельных точках графика.

Простым способом проверки основной гипотезы являются вычисления коэффициентов асимметрии (а) и коэффициентов эксцесса (е) эмпирических распределений, а также их сравнение с критериальными значениями. Надежность статистических выводов повышается при увеличении объёма выборочных данных. На рис. 3 приведены последовательности коэффициентов для 17 сечений градуировочной функции. Коэффициенты вычислены по результатам 100 испытаний в каждой точке. Критические значения коэффициентов для нашего примера равны |а| = 0,72 и |е| = 0,23.

Из рис. 3 можно сделать вывод о том, что рассеяние значений в точках графика, в целом, не

противоречит гипотезе нормальности, поскольку последовательности коэффициентов почти не имеют предпочтительной направленности. Коэффициенты случайным образом локализуются вблизи нулевой линии (показана пунктиром). Для нормального распределения, как известно, математическим ожиданием коэффициента асимметрии и коэффициента эксцесса является нуль. Судя по тому, что при всех сечениях коэффициенты асимметрии существенно ниже критического значения, можно уверенно говорить о симметричности распределения погрешностей градуирования. Возможно, что распределения погрешностей обладают небольшой остроконечностью по сравнению с нормальной кривой распределения. Этот вывод следует из наблюдающегося на рис. 3 небольшого поло-

Рис. 3. Коэффициенты эксцесса (1) и коэффициенты асимметрии (2) в точках градуировочного графика

жительного смещения центральной линии рассеяния коэффициентов эксцесса. Таким образом, из исследования модели обобщенной градуировочной функции фотометрического анализа методом Монте-Карло (2), можно сделать вывод о близком к нормальному распределении погрешностей градуирования. Поэтому вычисления доверительных интервалов для результатов фотометрического анализа с использованием коэффициентов Стьюдента можно считать вполне оправданными.

При выполнении стохастического моделирования была оценена быстрота сходимости выборочных кривых погрешностей (см. рис. 2) к математическому ожиданию кривой. За математическое ожидание кривой погрешностей примем расчитанную из ЗНО кривую. Близость результатов статистических испытаний с различным числом реализаций градуировки п к теоретической кривой оценим коэффициентом неопределенности 1 - Я2. Этот коэффициент характеризует долю вариации в выборке, которую не удалось описать теоретически. Нами установлено, что зависимость коэффициента неопределенности от числа реализаций градуировочной функции можно описать эмпирическим уравнением I - К2 = -2,3п-1 + 1,6п~/а -0,1. Из уравнения получаем, что при п = 213 следует ожидать практически полного совпадения теоретической и эмпирической кривых погрешностей. Таким образом, состоятельную оценку погрешностей фотометрического анализа можно получить только на довольно большом статистическом материале.

Рассмотрим возможности метода статистических испытаний для прогнозирования результатов регресионного анализа градуировочного графика и использования графика при определении концентраций фотометрируемых растворов. Для этого в качестве сценария выберем измерительную ситуацию рутинного анализа. Построение графика осуществляют при однократных измерениях оптических плотностей серии стандартных растворов. Концентрацию анализируемого раствора находят из графика по 3-4 результатам параллельных измерений. При выборе регрессионной модели следует принять во внимание то, что разброс оптических плотностей в различных точках градуировочного графика неодинаков, см. уравнение (8). В случае гетероекедастичного разброса рекомендуют использовать схему взвешенного метода наименьших квадратов (ВМНК). Однако в литературе мы не встретили четких указаний на причины, по которым классическая схема МНК, одним из условий применимости которой является требование гомоскеда-стичности разброса, менее предпочтительна. Эти причины можно установить при обработке одного и того же статистического материала, полученного методом Монте-Карло по сценарию рутинного анализа, двумя вариантами МНК - классическим и взвешенным.

В результате регрессионного анализа только одной реализации градуировочной функции получены следующие МНК-оценки: к = 4,979 при Бк = 0,023. При оценке тех же характеристик ВМНК получаем к = 5,000 при Бк = 0,016. Регрессии восстанавливали по 17 стандартным растворам. Концентрации в градуировочной серии возрастали в арифметической прогрессии, а оптические плотности изменялись столь же равномерно на интервале от 0,1 до 1,7 ед. В случае ВМНК статистические веса точек градуировочного графика находили с использованием рассчитанных по уравнению (5) дисперсий.

Дисперсии оценок к тем и другим методом статистически неразличимы по критерию Фишера при 1 %-ном уровне значимости. Однако при том же уровне значимости МНК-оценка к отличается от ВМНК-оценки по 1;-критерию. МНК-оценка коэффициента градуировочного графика смещена относительно действительного значения М(к) = 5,000, судя по 1>тесту при 5 %-ном уровне значимости. Тогда как взвешенный МНК дает оценку, которая не содержит систематической погрешности.

Теперь выясним, каким образом пренебрежение гетероскедастичностью может отразиться на качестве химического анализа. В таблице приведены результаты имитационного эксперимента по анализу 17 контрольных проб окрашенного вещества с различной концентрацией. Причем каждая аналитическая серия включала четыре раствора, т.е. для каждой пробы выполнено по четыре параллельных определения. Для обработки результатов использовали две разные градуировочные зависимости: одна была восстановлена простым МНК, а вторая - взвешенным. Полагаем, что контрольные растворы приготовлялись для анализа точно так же, как градуировочные.

Из таблицы видим, что действительные значения концентраций контрольных растворов как в случае ВМНК, так и в случае МНК не выходят за пределы доверительных интервалов, т. е. результаты анализа не содержат значимых систематических погрешностей. Предельные погрешности того и другого метода статистически не различаются, иными словами, и та и другая оценка

Сравнение результатов определения концентраций обладает одинаковой эффективностью. От-

контрольных растворов двумя методами сюда можно сделать вывод о том, что при

рутинных анализах использование простой схемы невзвешенного МНК вполне оправдано. Применение ВМНК предпочтительней, если исследовательской задачей является только определение молярной экстинкции. С другой стороны, следует иметь в виду, что сделанные нами выводы имеют статистический характер. Вполне вероятно, что при увеличении числа параллельных определений гипотеза о несмещенности МНК-оценок концентраций не найдет подтверждения, даже если систематические погрешности с практической точки зрения несущественны.

Обнаруженное нами достаточно высокое качество анализа на основе простой схемы классического МНК кажется особенно неожиданным, если принять во внимание то, что на интервале оптических плотностей 0,1 ч- 1,7 наблюдается весьма сильная гете-роскедастичность. О степени неоднородности данных можно судить по весовой функции, которая хорошо аппроксимируется полиномом w = 0,057А2 - 0,193А + 0,173. Из этого уравнения следует, что в крайних точках градуировки статистические веса различаются более чем в 20 раз. Однако обратим внимание на то, что градуировочные функции восстанавливали по 17 точкам графика, тогда как при анализе выполняли только 4 параллельных определения. Поэтому обнаруженное нами значимое различие МНК и ВМНК градуировочных функций и незначительное различие результатов анализа с использованием этих функций можно объяснить существенно различным числом степеней свободы, которыми располагали при построении статистических выводов.

Заключение

1. Предложен новый подход к стохастическому моделированию в фотометрическом анализе на основе метода Монте-Карло и закона накопления ошибок с использованием табличного процессора Excel.

2. По 100 реализациям градуировочной зависимости показано, что прогнозирование погрешностей аналитическим и статистическим методом взаимосогласованы.

3. Изучены коэффициенты асимметрии и эксцесса вдоль градуировочного графика. Найдено, что вариации погрешностей градуирования подчиняются закону распределения, близкому к нормальному.

4. Рассмотрено влияние гетероскедастичности разброса оптических плотностей при градуировании на качество анализа. Обнаружено, что при рутинных анализах использование простой схемы невзвешенного МНК не приводит к заметному снижению точности результатов анализа.

Литература

1. Бернштейн, И.Я. Спектрофотометрический анализ в органической химии / И.Я. Бернштейн, Ю.Л. Каминский. - Л.: Химия, 1986. - 200 с.

2. Булатов, М.И. Практическое руководство по фотометрическим методам анализа / М.И. Булатов, И.П. Калинкин. - Л.: Химия, 1986. - 432 с.

3. Гмурман, В.Е. Теория вероятностей и математическая статистика / В.Е. Гмурман. - М.: Высшая школа, 1977. - 470 с.

№ с", с", найдено (Р = 95 %)

п/и задано МНК ВМНК

1 0,020 0,021±0,002 0,021±0,002

2 0,040 0,041±0,001 0,041 ±0,001

3 0,060 0,061±0,003 0,061 ±0,003

4 0,080 0,080±0,004 0,080±0,004

5 0,100 0,098±0,004 0,098±0,004

6 0,120 0,122±0,006 0,121±0,006

7 0,140 0,140±0,006 0,139±0,006

8 0,160 0,163±0,003 0,162±0,003

9 0,180 0,181±0,006 0,180±0,006

10 0,200 0,201±0,002 0,200±0,002

11 0,220 0,219±0,008 0,218±0,008

12 0,240 0,242±0,002 0,241±0,002

13 0,260 0,262±0,008 0,261±0,008

14 0,280 0,281±0,010 0,280±0,010

15 0,300 0,307±0,015 0,306±0,015

16 0,320 0,325±0,013 0,323±0,013

17 0,340 0,340±0,026 0,339±0,026

4. Правдин, П В. Лабораторные приборы и оборудование из стекла / П.В. Правдин. - М.: Химия, 1988.-336 с.

5. Макарова, Н.В. Статистика в Excel / Н.В. Макарова, В.Я. Трофимец. - М.: Финансы и статистика, 2002. - 368 с.

PREDICTION OF ERRORS IN PHOTOMETRY WITH THE USE OF ACCUMULATION OF ERRORS LAW AND MONTE CARLO METHOD

During computing experiment, in combination of the accumulation of errors law and Monte Carlo method, the influence of solution-making errors, blank experiment errors and optical transmission measurement errors upon metrological performance of photometrical analysis has been studied. It has been shown that the results of prediction by analytical and statistical methods are interconsistent. The unique feature of Monte Carlo method has been found to enable prediction of the accumulation of errors law in photometry. For the version of routine analysis the influence of heteroscedasticity of dispersion along calibration curve upon analysis quality has been studied.

Keywords: photometric analysis, accumulation of errors law, calibration curve, metrological performance, Monte Carlo method, stochastic modeling.

Golovanov Vladimir Ivanovich - Dr. Sc. (Chemistry), Professor, Head of the Analytical Chemistry Subdepartment, South Ural State University.

Голованов Владимир Иванович - доктор химических наук, профессор, заведующий кафедрой Аналитической химии, Южно-Уральский государственный университет.

E-mail: [email protected]

Danilina Elena Ivanovna - PhD (Chemistry), Associate Professor, Analytical Chemistry Subdepartment, South Ural State University.

Данилина Елена Ивановна - кандидат химических наук, доцент, кафедра «Аналитическая химия», Южно-У ральский государственный университет.

при численном решении алгебраических уравнений - суммарное влияние округлений, сделанных на отдельных шагах вычислительного процесса, на точность полученного решения линейной алгебраич. системы. Наиболее распространенным способом априорной оценки суммарного влияния ошибок округления в численных методах линейной алгебры является схема т. н. обратного анализа. В применении к решению системы линейных алгебраич. уравнений

схема обратного анализа заключается в следующем. Вычисленное прямым методом Мрешение хуи не удовлетворяет (1), но может быть представлено как точное решение возмущенной системы

Качество прямого метода оценивается по наилучшей априорной оценке, к-рую можно дать для норм матрицы и вектора . Такие "наилучшие"и наз. соответственно матрицей и вектором эквивалентного возмущения для метода М.

Если оценки для и имеются, то теоретически ошибка приближенного решения может быть оценена неравенством

Здесь - число обусловленности матрицы А, а матричная норма в (3) предполагается подчиненной векторной норме

В действительности оценка для редко бывает известна, и основной смысл (2) состоит в возможности сравнения качества различных методов. Ниже приводится вид нек-рых типичных оценок для матрицы Для методов с ортогональными преобразованиями и арифметики с плавающей запятой (в системе (1) Аи bсчитаются действительными)

В этой оценке - относительная точность арифметич. операций в ЭВМ,- евклидова матричная норма, f(n) - функция вида , где п- порядок системы. Точные значения константы Си показателя kопределяются такими деталями вычислительного процесса, как способ округления, использование операции накопления скалярных произведений и т. д. Наиболее часто k=1 или 3/2.

В случае методов типа Гаусса в правую часть оценки (4) входит еще множитель , отражающий возможность роста элементов матрицы Ана промежуточных шагах метода по сравнению с первоначальным уровнем (такой рост отсутствует в ортогональных методах). Чтобы уменьшить значение , применяют различные способы выбора ведущего элемента, препятствующие возрастанию элементов матрицы.

Для квадратного корня метода, к-рый применяется обычно в случае положительно определенной матрицы А, получена наиболее сильная оценка

Существуют прямые методы (Жордана, окаймления, сопряженных градиентов), для к-рых непосредственное применение схемы обратного анализа не приводит к эффективным оценкам. В этих случаях при исследовании Н. п. применяются и иные соображения (см. - ).

Лит. : Givens W., "TJ. S. Atomic Energy Commiss. Repts. Ser. OR NL", 1954, № 1574; Wilkinson J. H., Rounding errors in algebraic processes, L., 1963; Уилкинсон Д ж.

X. Д. Икрамов.

Н. п. округления или погрешности метода возникает при решении задач, где решение является результатом большого числа последовательно выполняемых арифметич. операций.

Значительная часть таких задач связана с решением алгебраич. задач, линейных или нелинейных (см. выше). В свою очередь среди алгебраич. задач наиболее распространены задачи, возникающие при аппроксимации дифференциальных уравнений. Этим задачам свойственны нек-рые специфич. особенности.

Н. п. метода решения задачи происходит по тем же или по более простым законам, что и Н. п. вычислительной погрешности; Н. ,п. метода исследуется при оценке метода решения задачи.

При исследовании накопления вычислительной погрешности различают два подхода. В первом случае считают, что вычислительные погрешности на каждом шаге вносятся самым неблагоприятным образом и получают мажорантную оценку погрешности. Во втором случае считают, что эти погрешности случайны с определенным законом распределения.

Характер Н. п. зависит от решаемой задачи, метода решения и ряда других факторов, на первый взгляд могущих показаться несущественными; сюда относятся форма записи чисел в ЭВМ (с фиксированной запятой или с плавающей запятой), порядок выполнения арифметич. операций и т. д. Напр., в задаче вычисления суммы Nчисел

существенен порядок выполнения операций. Пусть вычисления производятся на машине с плавающей запятой с tдвоичными разрядами и все числа лежат в пределах . При непосредственном вычислении с помощью рекуррентной формулы мажорантная оценка погрешности имеет порядок 2 -t N. Можно поступить иначе (см. ). При вычислении попарных сумм (если N=2l+1 нечетно) полагают . Далее вычисляются их попарные суммы и т. д. При после тшагов образования попарных сумм по формулам

получают мажорантная оценка погрешности порядка

В типичных задачах величины а т вычисляются по формулам, в частности рекуррентным, или поступают последовательно в оперативную память ЭВМ; в этих случаях применение описанного приема приводит к увеличению загрузки памяти ЭВМ. Однако можно организовать последовательность вычислений так, что загрузка оперативной памяти не будет превосходить -log 2 N ячеек.

При численном решении дифференциальных уравнений возможны следующие случаи. При стремлении шага сетки hк нулю погрешность растет как где . Такие методы решения задач относят к классу неустойчивых. Их применение носит эпизодич. характер.

Для устойчивых методов характерен рост погрешности как Оценка погрешности таких методов обычно производится следующим образом. Строится уравнение относительно возмущения, вносимого или округлением, или погрешностями метода и затем исследуется решение этого уравнения (см. , ).

В более сложных случаях применяется метод эквивалентных возмущений (см. , ), развитый в отношении задачи исследования накопления вычислительной погрешности при решении дифференциальных уравнений (см. , , ). Вычисления по нек-рой расчетной схеме с округлениями рассматриваются как вычисления без округлений, но для уравнения с возмущенными коэффициентами. Сравнивая решение исходного сеточного уравнения с решением уравнения с возмущенными коэффициентами получают оценку погрешности.

Уделяется существенное внимание выбору метода по возможности с меньшими значениями qи A(h). При фиксированном методе решения задачи расчетные формулы обычно удается преобразовать к виду, где (см. , ). Это особенно существенно в случае обыкновенных дифференциальных уравнений, где число шагов в отдельных случаях оказывается очень большим.

Величина (h)может сильно расти с ростом промежутка интегрирования. Поэтому стараются применять методы по возможности с меньшим значением A(h). В случае задачи Коши ошибка округления на каждом конкретном шаге по отношению к последующим шагам может рассматриваться как ошибка в начальном условии. Поэтому нижняя грань (h)зависит от характеристики расхождения близких решений дифференциального уравнения, определяемого уравнением в вариациях.

В случае численного решения обыкновенного дифференциального уравнения уравнение в вариациях имеет вид

и потому при решении задачи на отрезке ( х 0 , X )нельзя рассчитывать на константу A(h)в мажорантной оценке вычислительной погрешности существенно лучшую, чем

Поэтому при решении этой задачи наиболее употребительны однощаговые методы типа Рунге - Кутта или методы типа Адамса (см. , ), где Н. п. в основном определяется решением уравнения в вариациях.

Для ряда методов главный член погрешности метода накапливается по подобному закону, в то время как вычислительная погрешность накапливается существенно быстрее (см. ). Область практич. применимости таких методов оказывается существенно уже.

Накопление вычислительной погрешности существенно зависит от метода, применяемого для решения сеточной задачи. Напр., при решении сеточных краевых задач, соответствующих обыкновенным дифференциальным уравнениям, методами стрельбы и прогонки Н. п. имеет характер A(h)h -q , где qодно и то же. Значения A(h)у этих методов могут отличаться настолько, что в определенной ситуации один из методов становится неприменимым. При решении методом пристрелки сеточной краевой задачи для уравнения Лапласа Н. п. имеет характер с 1/h , с >1, а в случае метода прогонки Ah -q . При вероятностном подходе к исследованию Н. п. в одних случаях априорно предполагают какой-то закон распределения погрешности (см. ), в других случаях вводят меру на пространстве рассматриваемых задач и, исходя из этой меры, получают закон распределения погрешностей округления (см. , ).

При умеренной точности решения задачи мажорантные и вероятностные подходы к оценке накопления вычислительной погрешности обычно дают качественно одинаковые результаты: или в обоих случаях Н. п. происходит в допустимых пределах, или в обоих случаях Н. п. превосходит такие пределы.

Лит. : Воеводин В. В., Вычислительные основы линейной алгебры, М., 1977; Шура-Бура М. Р., "Прикл. матем. и механ.", 1952, т. 16, № 5, с. 575-88; Бахвалов Н. С, Численные методы, 2 изд., М., 1975; Уилкинсон Дж. X., Алгебраическая проблема собственных значений, пер. с англ., М.. 1970; Бахвалов Н. С, в кн.: Вычислительные методы и программирование, в. 1, М., 1962, с, 69-79; Годунов С. К., Рябенький В. С, Разностные схемы, 2 изд., М., 1977; Бахвалов Н. С, "Докл. АН СССР", 1955, т. 104, № 5, с. 683-86; его же, "Ж. вычислит, матем. и матем. физики", 1964; т. 4, № 3, с. 399- 404; Лапшин Е. А., там же, 1971, т. 11, № 6, с.1425-36.

• - отклонения результатов измерений истинных значений измеряемой величины. Систематич...
• - отклонения метрологич. свойств или параметров средств измерений от поминальных, влияющее на погрешности результатов измерений...

  Естествознание. Энциклопедический словарь

• - отклонения результатов измерений от истинных значений измеряемой величины. Играют существенную роль при производстве ряда судебных экспертиз...

  Криминалистическая энциклопедия

• - : Смотри также: - погрешности средств измерений - погрешности измерений...
• - Смотри...

  Энциклопедический словарь по металлургии

• - отклонения метрологических параметров средств измерений от номинальных, влияющие на погрешности результатов измерений...

  Энциклопедический словарь по металлургии

• - "...Периодические погрешности - погрешности, значение которых является периодической функцией времени или перемещения указателя измерительного прибора.....

  Официальная терминология

• - "...Постоянные погрешности - погрешности, которые длительное время сохраняют свое значение, например в течение времени выполнения всего ряда измерений. Они встречаются наиболее часто.....

  Официальная терминология

• - "...Прогрессивные погрешности - непрерывно возрастающие или убывающие погрешности...

  Официальная терминология

• - см. Ошибки наблюдений...

  Энциклопедический словарь Брокгауза и Евфрона

• - ошибки измерений, отклонения результатов измерений от истинных значений измеряемых величин. Различают систематические, случайные и грубые П. и. ...
• - отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений, получаемых при помощи этих средств...

  Большая Советская энциклопедия

• - разность между результатами измерений и истинным значением измеряемой величины. Относительной погрешностью измерения называется отношение абсолютной погрешности измерения к истинному значению...

  Современная энциклопедия

• - отклонения результатов измерений от истинных значений измеряемой величины...

  Большой энциклопедический словарь

• - прил., кол-во синонимов: 3 исправивший устранивший неточности устранивший ошибки...

  Словарь синонимов

• - прил., кол-во синонимов: 4 исправлявший устранявший изъяны устранявший неточности устранявший ошибки...

  Словарь синонимов

"НАКОПЛЕНИЕ ПОГРЕШНОСТИ" в книгах

Технические погрешности

Из книги Звезды и немного нервно автора

Технические погрешности

Из книги Напрасные совершенства и другие виньетки автора Жолковский Александр Константинович

Технические погрешности Рассказы об успешном противостоянии силе не так неправдоподобны, как мы подспудно боимся. Наезд обычно предполагает пассивность жертвы, а потому продумывается лишь на шаг вперед и контрудара не выдерживает. Папа рассказывал об одном таком

Грешки и погрешности

Из книги Как NASA показало Америке Луну автора Рене Ральф

Грешки и погрешности Несмотря на всю фиктивность своей космической навигации, NASA кичилось потрясающей точностью во всем, что бы ни делало. Девять раз подряд капсулы Аполлонов идеально ложились на лунную орбиту, не нуждаясь в серьезной корректировке курса. Лунный модуль,

Первоначальное накопление капитала. Насильственное обезземеливание крестьян. Накопление богатств.

автора

Первоначальное накопление капитала. Насильственное обезземеливание крестьян. Накопление богатств. Капиталистическое производство предполагает два основных условия: 1) наличие массы неимущих людей, лично свободных и в то же время лишённых средств производства и

Социалистическое накопление. Накопление и потребление в социалистическом обществе.

Из книги Политическая экономия автора Островитянов Константин Васильевич

Социалистическое накопление. Накопление и потребление в социалистическом обществе. Источником расширенного социалистического воспроизводства является социалистическое накопление. Социалистическое накопление есть использование части чистого дохода общества,

Погрешности измерений

БСЭ

Погрешности средств измерений

Из книги Большая Советская Энциклопедия (ПО) автора БСЭ

Погрешности УЗИ

Из книги Восстановление щитовидной железы Руководство для пациентов автора Ушаков Андрей Валерьевич

Погрешности УЗИ Когда из С.-Петербурга ко мне приехала на консультацию пациентка, я увидел сразу три протокола ультразвукового обследования. Все они были сделаны разными специалистами. По-разному описаны. При этом даты исследований отличались друг от друга почти

Приложение 13 Речевые погрешности

Из книги Искусство добиваться своего автора Степанов Сергей Сергеевич

Приложение 13 Речевые погрешности Даже безобидные на первый взгляд фразы зачастую могут стать серьезным барьером в продвижении по службе. Известный американский специалист по маркетингу Джон Р. Грехем составил список выражений, употребление которых, по его наблюдениям,

Речевые погрешности

Из книги Сколько вы стоите [Технология успешной карьеры] автора Степанов Сергей Сергеевич

Речевые погрешности Даже безобидные на первый взгляд фразы зачастую могут стать серьезным барьером в продвижении по службе. Известный американский специалист по маркетингу Джон Р. Грехем составил список выражений, употребление которых, по его наблюдениям, не позволило

Губительные погрешности

Из книги Чёрный лебедь [Под знаком непредсказуемости] автора Талеб Нассим Николас

Губительные погрешности У погрешностей есть такое губительное свойство: чем они значительнее, тем больше их маскирующее воздействие.Никто не видит дохлых крыс, и поэтому чем смертельнее риск, тем менее он явен, ведь пострадавшие исключаются из числа свидетелей. Чем

Погрешности при ориентировании

Из книги Азбука туризма автора Бардин Кирилл Васильевич

Погрешности при ориентировании Итак, обычная задача на ориентирование, которую приходится решать туристу, состоит в том, что надо прийти из одного пункта в другой, пользуясь только компасом и картой. Местность незнакомая и к тому же закрытая, т. е. лишенная сколько-нибудь

Погрешности: философия

Из книги автора

Погрешности: философия На интуитивном уровне мы понимаем, что знание наше во многих случаях не точно. Можно осторожно предположить, что точным наше знание вообще может быть только при дискретной шкале. Можно точно знать, сколько шариков в мешке, но нельзя - каков их вес,

Погрешности: модели

Из книги автора

Погрешности: модели Когда мы что-то измеряем, имеющуюся к моменту начала измерений информацию (как осознанная, так и неосознанная) удобно представить в виде моделей объекта или явления. Модель «нулевого уровня» - это модель наличия величины. Мы верим в то, что она есть -

Погрешности: что и как контролировать

Из книги автора

Погрешности: что и как контролировать Выбор контролируемых параметров, схемы измерений, метода и объема контроля делается с учетом выходных параметров изделия, его конструкции и технологии, требований и потребностей того, кто применяет контролируемые изделия. Опять же,

Под погрешностью измерения будем понимать совокупность всех ошибок измерения.

Ошибки измерений можно классифицировать на следующие виды:

Абсолютные и относительные,

Положительные и отрицательные,

Постоянные и пропорциональные,

Случайные и систематические,

Абсолютная ошибка А y ) определяется как разность следующих величин:

А y = y i - y ист.  y i -y ,

где: y i – единичный результат измерения;y ист. – истинный результат измерения;y – среднее арифметическое значение результата измерения (далее среднее).

Постоянной называется абсолютная ошибка, которая не зависит от значения измеряемой величины (y  y ).

Ошибка пропорциональная , если названная зависимость существует. Характер ошибки измерения (постоянная или пропорциональная) определяется после проведения специальных исследований.

Относительная ошибка единичного результата измерения (В y ) рассчитывается как отношение следующих величин:

Из этой формулы следует, что величина относительной ошибки зависит не только от величины абсолютной ошибки, но и от значения измеряемой величины. При неизменности измеряемой величины (y ) относительную ошибку измерения можно уменьшить только за счет снижения величины абсолютной ошибки (А y ). При постоянстве абсолютной ошибки измерения для уменьшения относительной ошибки измерения можно использовать прием увеличения значения измеряемой величины.

Знак ошибки (положительный или отрицательный) определяется разницей между единичным и полученным (средним арифметическим) результатом измерения:

y i -y > 0 (ошибка положительная );

y i -y < 0 (ошибка отрицательная ).

Грубая ошибка измерения (промах) возникает при нарушении методики измерения. Результат измерения, содержащий грубую ошибку, обычно значительно отличается по величине от других результатов. Наличие грубых ошибок измерения в выборке устанавливается только методамиматематической статистики (при числе повторений измерения n >2). С методами обнаружения грубых ошибок познакомьтесь самостоятельно в .

К случайным ошибкам относят ошибки, которые не имеют постоянной величины и знака. Такие ошибки возникают под действием следующих факторов: не известных исследователю; известных, но нерегулируемых; постоянно изменяющихся.

Случайные ошибки можно оценить только после проведения измерений.

Количественной оценкой модуля величины случайной ошибки измерения могут являться следующие параметры: выборочная дисперсия единичных значений и среднего значения; выборочные абсолютные стандартные отклонения единичных значений и среднего значения; выборочные относительные стандартные отклонения единичных значений и среднего значения; генеральная дисперсия единичных значений ), соответственно, и др.

Случайные ошибки измерения невозможно исключить, их можно только уменьшить. Один из основных способов уменьшения величины случайной ошибки измерения – это увеличение числа (объема выборки) единичных измерений (увеличение величины n ). Объясняется это тем, что величина случайных ошибок обратно пропорциональна величинеn , например:

.

Систематические ошибки – это ошибки с неизменными величиной и знаком или изменяющиеся по известному закону. Эти ошибки вызываются постоянными факторами. Систематические ошибки можно количественно оценивать, уменьшать и даже исключать.

Систематические ошибки классифицируют на ошибки I,IIиIIIтипов.

К систематическим ошибкам I типа относят ошибки известного происхождения, которые могут быть до проведения измерения оценены путем расчета. Эти ошибки можно исключить, вводя их в результат измерения в виде поправок. Примером ошибки такого типа является ошибка при титрометрическом определении объемной концентрации раствора, если титрант был приготовлен при одной температуре, а измерение концентрации проводилось при другой. Зная зависимость плотности титранта от температуры, можно до проведения измерения рассчитать изменение объемной концентрации титранта, связанное с изменением его температуры, и эту разницу учесть в виде поправки в результате измерения.

Систематические ошибки II типа – это ошибки известного происхождения, которые можно оценить только в ходе эксперимента или в результате проведения специальных исследований. К этому типу ошибок относят инструментальные (приборные), реактивные, эталонные и др. ошибки. Познакомьтесь с особенностями таких ошибок самостоятельно в .

Любой прибор при его применении в процедуре измерения вносит в результат измерения свои приборные ошибки. При этом часть этих ошибок случайная, а другая часть – систематическая. Случайные ошибки приборов отдельно не оценивают, их оценивают в общей совокупности со всеми другими случайными ошибками измерения.

Каждый экземпляр любого прибора имеет свою персональную систематическую ошибку. Для того чтобы оценить эту ошибку, необходимо проводить специальные исследования.

Наиболее надежный способ оценки приборной систематической ошибки IIтипа – это сверка работы приборов по эталонам. Для мерной посуды (пипетка, бюретка, цилиндры и др.) проводят специальную процедуру – калибровку.

На практике наиболее часто требуется не оценить, а уменьшить или исключить систематическую ошибку IIтипа. Самыми распространенными методами уменьшения систематических ошибок являютсяметоды релятивизации и рандомизации .Познакомьтесь с этими методами самостоятельно в .

К ошибкам III типа относят ошибки неизвестного происхождения. Эти ошибки можно обнаружить только после устранения всех систематических ошибокIиIIтипов.

К прочим ошибкам отнесем все другие виды ошибок, не рассмотренные выше (допускаемые, возможные предельные ошибки и др.).

Понятие возможных предельных ошибок применяется в случаях использования средств измерения и предполагает максимально возможную по величине инструментальную ошибку измерения (реальное же значение ошибки может быть меньше величины возможной предельной ошибки).

При использовании средств измерения можно рассчитать возможную предельную абсолютную (
) или относительную (
) погрешность измерения. Так, например, возможная предельная абсолютная погрешность измерения находится как сумма возможных предельных случайных (
) и неисключенных систематических (
) ошибок:

=
+

При выборках малого объема (n 20) неизвестной генеральной совокупности, подчиняющейся нормальному закону распределения, случайные возможные предельные ошибки измерений можно оценить следующим образом:

= =
,

где: – доверительный интервал для соответствующей вероятностиР ;

–квантиль распределения Стьюдента для вероятности Р и выборки объемомn или при числе степеней свободыf = n – 1.

Абсолютная возможная предельная погрешность измерения в этом случае будет равна:

=
+
.

Если результаты измерений не подчиняются нормальному закону распределения, то оценка погрешностей проводится по другим формулам.

Определение величины
зависит от наличия у средства измерения класса точности. Если средство измерения не имеет класса точности, тоза величину
можно принять минимальную цену деления шкалы (или ее половину) средства измерения . Для средства измерения с известным классом точности за величину
можно принять абсолютнуюдопускаемую систематическую ошибку средства измерения (
):


.

Величина
рассчитывается исходя из формул, приведенных в табл. 2.

Для многих средств измерения класс точности указывается в виде чисел а 10 n , гдеа равно 1; 1,5; 2; 2,5; 4; 5; 6 иn равно 1; 0; -1; -2 и т.д., которые показывают величину возможной предельной допускаемой систематической ошибки (Е y , доп. ) и специальных знаков, свидетельствующих о ее типе (относительная, приведенная, постоянная, пропорциональная).

Если известны составляющие абсолютной систематической ошибки среднего арифметического результата измерения (например, приборная ошибка, ошибка метода и др.), то ее можно оценить по формуле

,

где: m – число составляющих систематическую ошибку среднего результата измерения;

k – коэффициент, определяемый вероятностьюР и числомm ;

–абсолютная систематическая ошибка отдельной составляющей.

Отдельными составляющими погрешности можно пренебрегать при выполнении соответствующих условий.

Таблица 2

Примеры обозначения классов точности средств измерения

Обозначение класса точности		Формула расчета и значение предельной допускаемой систематической ошибки	Характеристика систематической ошибки
в документации	на средстве измерения
			Приведенная допускаемая систематическая ошибка в процентах от номинального значения измеряемой величины, которое определяется типом шкалы средства измерения
			Приведенная допускаемая систематическая ошибка в процентах от длины использованной шкалы средства измерения (А) при получении единичных значений измеряемой величины
			Постоянная относительная допускаемая систематическая ошибка в процентах от полученного единичного значения измеряемой величины
		c = 0,02; d = 0,01	Пропорциональная относительная допускаемая систематическая ошибка в долях от полученного единичного значения измеряемой величины, которая возрастает при увеличении конечного значения диапазона измерения данным средством измерения (y k) или уменьшении единичного значения измеряемой величины (y i)

Систематическими ошибками можно пренебрегать, если выполняется неравенство

0,8.

В этом случае принимают



.

Случайными ошибками можно пренебречь при условии

8.

Для этого случая

.

Чтобы общая погрешность измерения определялась только систематическими ошибками, увеличивают число повторных измерений. Минимально необходимое для этого число повторных измерений (n min) можно рассчитать только при известном значении генеральной совокупности единичных результатов по формуле

.

Оценка погрешностей измерения зависит не только от условий измерения, но и от типа измерения (прямое или косвенное).

Деление измерений на прямые и косвенные достаточно условно. В дальнейшем под прямыми измерениями будем понимать измерения значения которых берут непосредственно из опытных данных, например, считывают со шкалы прибора (широко известный пример прямого измерения –измерение температуры термометром). Ккосвенным измерениям будем относить такие, результат которых получают на основании известной зависимости между искомой величиной и величинами, определяемыми в результате прямых измерений. При этомрезультат косвенного измеренияполучают расчетным путем как значение функции , аргументами которой являются результаты прямых измерений (x 1 ,x 2 , …,x j,. …,x k).

Необходимо знать, что ошибки косвенных измерений всегда больше, чем ошибки отдельных прямых измерений.

Ошибки косвенных измерений оцениваются по соответствующим законам накопления ошибок (приk 2).

Закон накопления случайных ошибок косвенных измерений выглядит следующим образом:

.

Закон накопления возможных предельных абсолютных систематических ошибок косвенных измерений представляется следующими зависимостями:

;
.

Закон накопления возможных предельных относительных систематических ошибок косвенных измерений имеет следующий вид:

;

.

В случаях, когда искомая величина (y ) рассчитывается как функция результатов нескольких независимых прямых измерений вида
, закон накопления предельных относительных систематических ошибок косвенных измерений принимает более простой вид:

;
.

Ошибки и погрешности измерений определяют их точность, воспроизводимость и правильность.

Точность тем выше, чем меньше величина погрешности измерения.

Воспроизводимость результатов измерений улучшается при уменьшении случайных ошибок измерений.

Правильность результата измерений увеличивается с уменьшением остаточных систематических ошибок измерений.

Более подробно с теорией ошибок измерений и их особенностями познакомьтесь самостоятельно . Обращаю ваше внимание на то, что современные формы представления конечных результатов измерений обязательно требуют приведения ошибок или погрешностей измерения (вторичных данных). При этом погрешности и ошибки измерений должны представляться числами, которые содержат не более двух значащих цифр .

Что такое "НАКОПЛЕНИЕ ПОГРЕШНОСТИ"? Как правильно пишется данное слово. Понятие и трактовка.

НАКОПЛЕНИЕ ПОГРЕШНОСТИ при численном решении алгебраических уравнений - суммарное влияние округлений, сделанных на отдельных шагах вычислительного процесса, на точность полученного решения линейной алгебраич. системы. Наиболее распространенным способом априорной оценки суммарного влияния ошибок округления в численных методах линейной алгебры является схема т. н. обратного анализа. В применении к решению системы линейных алгебраич. уравнений схема обратного анализа заключается в следующем. Вычисленное прямым методом Мрешение хуи не удовлетворяет (1), но может быть представлено как точное решение возмущенной системы Качество прямого метода оценивается по наилучшей априорной оценке, к-рую можно дать для норм матрицы и вектора. Такие "наилучшие"и наз. соответственно матрицей и вектором эквивалентного возмущения для метода М. Если оценки для и имеются, то теоретически ошибка приближенного решения может быть оценена неравенством Здесь - число обусловленности матрицы А, а матричная норма в (3) предполагается подчиненной векторной норме В действительности оценка для редко бывает известна, и основной смысл (2) состоит в возможности сравнения качества различных методов. Ниже приводится вид нек-рых типичных оценок для матрицы Для методов с ортогональными преобразованиями и арифметики с плавающей запятой (в системе (1) Аи bсчитаются действительными) В этой оценке - относительная точность арифметич. операций в ЭВМ,- евклидова матричная норма, f(n) - функция вида, где п- порядок системы. Точные значения константы Си показателя kопределяются такими деталями вычислительного процесса, как способ округления, использование операции накопления скалярных произведений и т. д. Наиболее часто k=1 или 3/2. В случае методов типа Гаусса в правую часть оценки (4) входит еще множитель, отражающий возможность роста элементов матрицы Ана промежуточных шагах метода по сравнению с первоначальным уровнем (такой рост отсутствует в ортогональных методах). Чтобы уменьшить значение, применяют различные способы выбора ведущего элемента, препятствующие возрастанию элементов матрицы. Для квадратного корня метода, к-рый применяется обычно в случае положительно определенной матрицы А, получена наиболее сильная оценка Существуют прямые методы (Жордана, окаймления, сопряженных градиентов), для к-рых непосредственное применение схемы обратного анализа не приводит к эффективным оценкам. В этих случаях при исследовании Н. п. применяются и иные соображения (см. - ). Лит.: Givens W., "TJ. S. Atomic Energy Commiss. Repts. Ser. OR NL", 1954, № 1574; Wilkinson J. H., Rounding errors in algebraic processes, L., 1963; Уилкинсон Д ж. устойчивость в прямых методах линейной алгебры, М., 1969; его же, Вычислительные основы линейной алгебры, М., 1977; Peters G., Wilkinsоn J. H., "Communs Assoc. Comput. Math.", 1975, v. 18, № 1, p. 20-24; Вrоуden C. G., "J. Inst. Math, and Appl.", 1974, v. 14, № 2, p. 131-40; Reid J. К., в кн.: Large Sparse Sets of Linear Equations, L.- N. Y., 1971, p. 231 - 254; Икрамов Х. Д., "Ж. вычисл. матем. и матем. физики", 1978, т. 18, № 3, с. 531-45. X. Д. Икрамов. Н. п. округления или погрешности метода возникает при решении задач, где решение является результатом большого числа последовательно выполняемых арифметич. операций. Значительная часть таких задач связана с решением алгебраич. задач, линейных или нелинейных (см. выше). В свою очередь среди алгебраич. задач наиболее распространены задачи, возникающие при аппроксимации дифференциальных уравнений. Этим задачам свойственны нек-рые специфич. особенности. Н. п. метода решения задачи происходит по тем же или по более простым законам, что и Н. п. вычислительной погрешности; Н. ,п. метода исследуется при оценке метода решения задачи. При исследовании накопления вычислительной погрешности различают два подхода. В первом случае считают, что вычислительные погрешности на каждом шаге вносятся самым неблагоприятным образом и получают мажорантную оценку погрешности. Во втором случае считают, что эти погрешности случайны с определенным законом распределения. Характер Н. п. зависит от решаемой задачи, метода решения и ряда других факторов, на первый взгляд могущих показаться несущественными; сюда относятся форма записи чисел в ЭВМ (с фиксированной запятой или с плавающей запятой), порядок выполнения арифметич. операций и т. д. Напр., в задаче вычисления суммы Nчисел существенен порядок выполнения операций. Пусть вычисления производятся на машине с плавающей запятой с tдвоичными разрядами и все числа лежат в пределах. При непосредственном вычислении с помощью рекуррентной формулы мажорантная оценка погрешности имеет порядок 2-tN. Можно поступить иначе (см. ). При вычислении попарных сумм (если N=2l+1 нечетно) полагают. Далее вычисляются их попарные суммы и т. д. При после тшагов образования попарных сумм по формулам получают мажорантная оценка погрешности порядка В типичных задачах величины а т вычисляются по формулам, в частности рекуррентным, или поступают последовательно в оперативную память ЭВМ; в этих случаях применение описанного приема приводит к увеличению загрузки памяти ЭВМ. Однако можно организовать последовательность вычислений так, что загрузка оперативной памяти не будет превосходить -log2N ячеек. При численном решении дифференциальных уравнений возможны следующие случаи. При стремлении шага сетки hк нулю погрешность растет как где. Такие методы решения задач относят к классу неустойчивых. Их применение носит эпизодич. характер. Для устойчивых методов характерен рост погрешности как Оценка погрешности таких методов обычно производится следующим образом. Строится уравнение относительно возмущения, вносимого или округлением, или погрешностями метода и затем исследуется решение этого уравнения (см. , ). В более сложных случаях применяется метод эквивалентных возмущений (см. , ), развитый в отношении задачи исследования накопления вычислительной погрешности при решении дифференциальных уравнений (см. , , ). Вычисления по нек-рой расчетной схеме с округлениями рассматриваются как вычисления без округлений, но для уравнения с возмущенными коэффициентами. Сравнивая решение исходного сеточного уравнения с решением уравнения с возмущенными коэффициентами получают оценку погрешности. Уделяется существенное внимание выбору метода по возможности с меньшими значениями qи A(h). При фиксированном методе решения задачи расчетные формулы обычно удается преобразовать к виду, где (см. , ). Это особенно существенно в случае обыкновенных дифференциальных уравнений, где число шагов в отдельных случаях оказывается очень большим. Величина (h)может сильно расти с ростом промежутка интегрирования. Поэтому стараются применять методы по возможности с меньшим значением A(h). В случае задачи Коши ошибка округления на каждом конкретном шаге по отношению к последующим шагам может рассматриваться как ошибка в начальном условии. Поэтому нижняя грань (h)зависит от характеристики расхождения близких решений дифференциального уравнения, определяемого уравнением в вариациях. В случае численного решения обыкновенного дифференциального уравнения уравнение в вариациях имеет вид и потому при решении задачи на отрезке (х 0 , X)нельзя рассчитывать на константу A(h)в мажорантной оценке вычислительной погрешности существенно лучшую, чем Поэтому при решении этой задачи наиболее употребительны однощаговые методы типа Рунге - Кутта или методы типа Адамса (см. , ), где Н. п. в основном определяется решением уравнения в вариациях. Для ряда методов главный член погрешности метода накапливается по подобному закону, в то время как вычислительная погрешность накапливается существенно быстрее (см. ). Область практич. применимости таких методов оказывается существенно уже. Накопление вычислительной погрешности существенно зависит от метода, применяемого для решения сеточной задачи. Напр., при решении сеточных краевых задач, соответствующих обыкновенным дифференциальным уравнениям, методами стрельбы и прогонки Н. п. имеет характер A(h)h-q, где qодно и то же. Значения A(h)у этих методов могут отличаться настолько, что в определенной ситуации один из методов становится неприменимым. При решении методом пристрелки сеточной краевой задачи для уравнения Лапласа Н. п. имеет характер с 1/h, с>1, а в случае метода прогонки Ah-q. При вероятностном подходе к исследованию Н. п. в одних случаях априорно предполагают какой-то закон распределения погрешности (см. ), в других случаях вводят меру на пространстве рассматриваемых задач и, исходя из этой меры, получают закон распределения погрешностей округления (см. , ). При умеренной точности решения задачи мажорантные и вероятностные подходы к оценке накопления вычислительной погрешности обычно дают качественно одинаковые результаты: или в обоих случаях Н. п. происходит в допустимых пределах, или в обоих случаях Н. п. превосходит такие пределы. Лит.: Воеводин В. В., Вычислительные основы линейной алгебры, М., 1977; Шура-Бура М. Р., "Прикл. матем. и механ.", 1952, т. 16, № 5, с. 575-88; Бахвалов Н. С, Численные методы, 2 изд., М., 1975; Уилкинсон Дж. X., Алгебраическая проблема собственных значений, пер. с англ., М.. 1970; Бахвалов Н. С, в кн.: Вычислительные методы и программирование, в. 1, М., 1962, с, 69-79; Годунов С. К., Рябенький В. С, Разностные схемы, 2 изд., М., 1977; Бахвалов Н. С, "Докл. АН СССР", 1955, т. 104, № 5, с. 683-86; его же, "Ж. вычислит, матем. и матем. физики", 1964; т. 4, № 3, с. 399- 404; Лапшин Е. А., там же, 1971, т. 11, № 6, с.1425-36. Н. С. Бахвалов.

Напечатать